算数や数学でつまずく子を見ていると、
「計算ができない」以前に、
「どこを見て考えればよいか分からない」状態
に陥っていることが少なくありません。
点描写は、算数・数学で「どこを見るべきか分からない」という生徒に最も効果的な思考基盤の作り方です。
Willbeの強みは、小学生から高校生まで一貫して塾長の光庵が指導している点にあります。
本記事では、点描写で何が育つか・具体的な指導法・家庭での練習方法まで徹底解説します。
点描写が具体的に数学のどのような点において役立つのか
① 図形分野（平面・立体）
- 図形を「面」や「形」ではなく構成要素（点）に分解して考えられる
- 頂点・交点・中点・端点など重要点を見落としにくくなる
- 補助線を引くべき場所（点）に気づきやすくなる
- 「どこが変わって、どこが変っていないか」を点で追える
- 合同・相似の対応関係を点対応として把握できる
- 回転・移動・対称移動を点の動きとして理解できる
- 図形の一部を動かす問題（可動点）に強くなる
- 面積比・長さ比を点の位置関係から導ける
- 作図問題で「何を決めれば図が定まるか」が明確になる
- 座標化する前段階として、点を意識できる
作図問題で「何を決めれば図が定まるか」が明確になる
２点の座標が分かれば直線が描けます。
→しかし、
当たり前すぎて、
このことを理解できている中学生は、
少ないのです。
当たり前のことを定着させるのが一番難しいのです。
この点については、後述します。
② 座標・関数分野
- グラフを「線」ではなく点の集合として理解できる
- 表 ⇄ グラフ ⇄ 式の対応がスムーズになる
- 一次関数・二次関数の変化を「点の動き」として捉えられる
- 交点の意味（解・条件成立点）を直感的に理解できる
- 最大値・最小値を「最も高い／低い点」として捉えられる
- 変数が増えたときも「状態＝点」として考えられる
- グラフの読み取り問題で「どの点を読むか」が明確になる
- 離散的なデータと連続的な変化の違いを理解できる
- 条件付き最大・最小問題で場合分けがしやすくなる
③ 数量関係・文章題
- 状況を「点（状態）」としてモデル化できる
- 時刻・位置・個数などを瞬間の点として捉えられる
- 「途中の状態」を想像しやすくなる
- 変化の前後を点で比較できる
- 比例・反比例の関係を点の並びとして理解できる
- 速さ・距離・時間の関係を点で整理できる
- 文章題を図に起こす力が上がる
- 条件が複数ある問題で「満たす点」を探す発想が持てる
④ 思考力・問題解決力
- 全体を一気に見ようとせず、局所（点）から考えられる
- 「まずどこを見るか」がはっきりする
- 見当違いな計算を減らせる
- 試行錯誤がしやすくなる（点を動かす）
- 抽象的な問題を具体化できる
- 図や条件を静止画ではなく動的に捉えられる
- 「なぜそうなるか」を説明しやすくなる
- 論理の飛躍が減る
「局所（点）から考えられる」
→このことについて後述いたします。
⑤ 記述・説明・証明
- 図形問題の説明が「点Aが〜」と明確になる
- 条件の根拠を点の位置関係で説明できる
- 証明の流れを「点→関係→結論」で整理できる
- 採点者に伝わる答案になりやすい
- 無駄な言葉が減り、論理が締まる
⑥ 学習初期（小学生）での効果
- 数や図形への視線が定まる
- 漠然とした「なんとなく分かった」を減らせる
- 数を「並び」や「位置」として捉えられる
- 図形の名前暗記に頼らなくなる
- 集中が持続しやすくなる
- 算数への抵抗感が減る
数や図形への視線が定まる
中学生を指導していて気になることは、
ｘ座標を「1番目、２番目、３番目の点」という風に順番に数えなければ点を決めれないお子様が多い
という点です。
慣れれば問題ないことなのですが、点描写を繰り返し瞬間的に３番目を把握できるようになっているお子様に比べて、
問題を解くスピードは圧倒的に遅くなります。
図形の名前暗記に頼らなくなる
小学１年～４年生で、
・長方形
・正方形
・ひし形
・平行四辺形
の特徴を習います。
テストでは、暗記させられます。
☝このような図形の特徴を言葉で覚えきれるものではありません。
右側の図で覚えれば、すぐに覚えられます。
⑦ 中学・高校・入試での効果
- 難問でも「手を付ける入口」が見つかる
- 図形×関数の融合問題に強くなる
- 場合分けが整理される
- ケアレスミスが減る
- 時間短縮につながる
- 思考過程が安定する
点描写を指導するうえでの注意点
小学受験などで点描写を訓練しているにも関わらず、図形感覚が乏しい子がいます。
そういった場合を防ぐ指導の注意点について、「点描写を教えるときに陥りやすい落とし穴」も含めて、まとめて参ります。
① 技法化しすぎない（最重要）
- 点描写は「テクニック」ではなくものの見方であることを忘れない
- 「ここに点を打て」と型で教えすぎない
- 正解の点だけをなぞらせない
- 点を打つ理由を必ず言語化させる
- 点を打たない自由も認める
「ここに点を打て」と型で教えすぎない
中学入試で取り扱われるような問題、
または、高校入試で扱われる図形についても、
図形の書き方を公式化するほか指導方法が許されません。
時間がないからです。
しかし、「書き方」すら全て公式化されていては図形は得意になりきらないように思います。
② 量より“意味”を優先する
- 点の数が多ければ良いわけではない
- 重要でない点を増やしすぎない
- 「その点は何を表しているか」を常に確認する
- 装飾的な点描写にならないよう注意
- 一点で状況が決まることもあると伝える
③ 子どもの視線を先回りしない
- 先に大人が重要点を示さない
- 「どこが気になる？」とまず聞く
- 間違った点の取り方も否定しない
- その点を取った理由を聞く
- 修正は“比較”で行う（点Aと点B、どちらがよいか）
④ 図形名・公式に逃がさない
- 「三角形だから」ではなく「どの点がどう関係するか」を問う
- 図形の名前を言わせて終わらせない
- 公式適用前に点の関係を確認する
- 面積・長さを出す前に「基準点」を意識させる
- 暗記型の処理に戻らせない
⑤ 動きを伴わせる
- 点を「固定された印」だと思わせない
- 動く点として想像させる
- 実際に指でなぞらせる
- 図を回転・反転させて点の移動を追わせる
- 「この点が動いたら何が変わる？」と問う
⑥ 言葉とセットで指導する
- 点を打ったら必ず説明させる
- 「なんとなく」を許さない
- 短い言葉でよいので理由を言わせる
- 正確な専門用語より、意味が通る言葉を優先
- 教師が言語化しすぎない
⑦ 書かせすぎない・描かせすぎない
- 点描写が作業化すると集中が切れる
- ノートを汚すことが目的にならないよう注意
- 必要最小限の点で止める勇気
- 頭の中だけで点を想像する練習も入れる
→順序数ではなく量で座標を示せるように。 - 黒板・プリント・空中（イメージ）を使い分ける
⑧ 年齢・理解段階に応じてレベル調整
- 低学年：位置・順番・端点から
- 中学年：交点・中点・基準点
- 高学年：可動点・不変点
- 中学生：条件を満たす点・場合分け
- 一気に抽象化しない
⑨ 正解より“過程”を評価する
- 点の取り方が筋道立っていれば評価する
- 答えが間違っていても思考は褒める
- 「良い点の取り方だった」と具体的に返す
- 点→関係→結論の流れを重視する
- 結果主義に引き戻さない
⑩ 他分野とつなげる
- 数直線の点と結びつける
- グラフの点と関連づける
- 文章題の「状態」を点で表す
- 日常の位置関係（席・地図）と結びつける
- 算数だけの特殊技能にしない
⑪ 失敗例を共有する
- 「点を打ちすぎると見えなくなる」例を見せる
- 間違った点描写の図をあえて提示する
- どこが違うかを話し合う
- 正解図と比較する
- 思考の違いに気づかせる
どこが違うかを話し合う
勉強が苦手な子あるあるランキング1位。
は、「答えが違うと言われれば全て消す。」です。
まず自分でどこがどう違うか分かってからでないと「タマタマ」の繰り返しです。
Willbeでは、点描写で間違えた場合、違う部分に○の印をつけてもらっている場合も多くあります。
⑫ 指導者自身が点で考えているかを点検する
- 自分の説明が面や式に偏っていないか
- 黒板で点を意識して書いているか
- 無意識に答えの点を示していないか
- 生徒の点描写を奪っていないか
- 「待つ」時間を取れているか
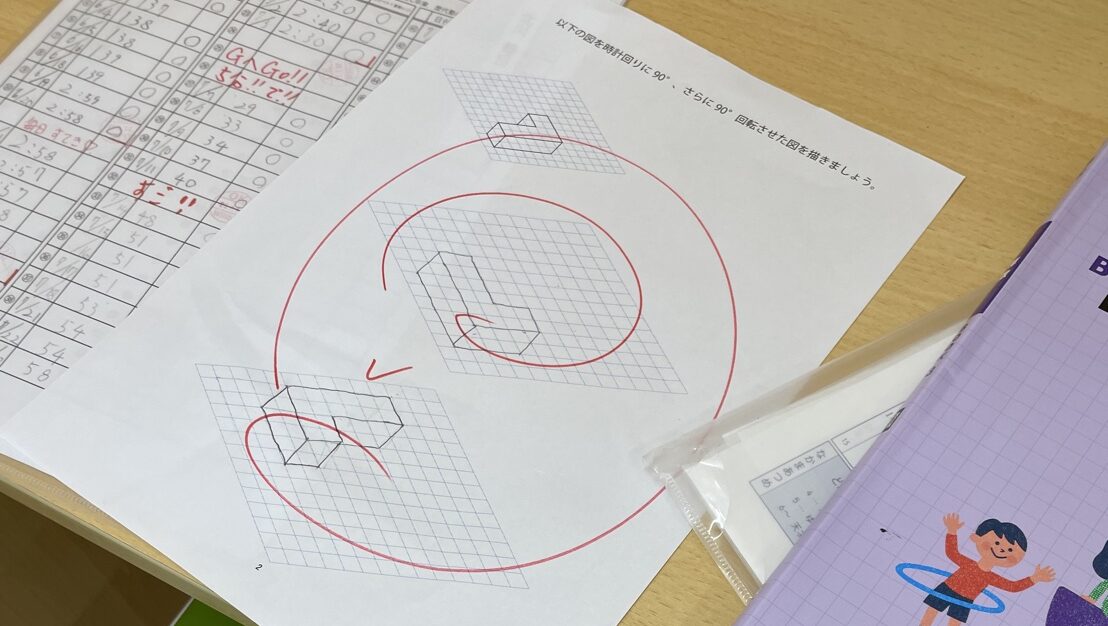
点描写の少し先
Willbe小学部では、点描写の先のルーティンとして、東京都「ZENT進学塾」武田先生が作成された投影図プリントも行っております。武田先生のプリントを使用して、以下の2点についてお話いたします。
・作図問題で「何を決めれば図が定まるか」が明確になる
・全体を一気に見ようとせず、局所（点）から考えられる
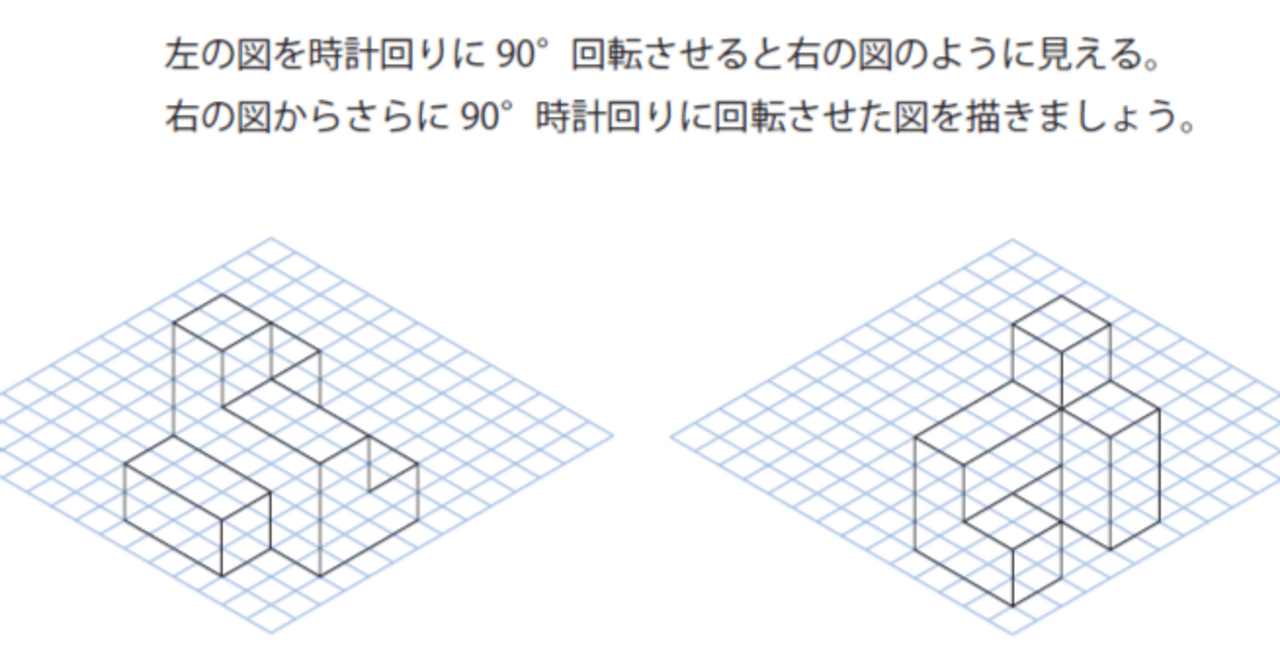
投影図
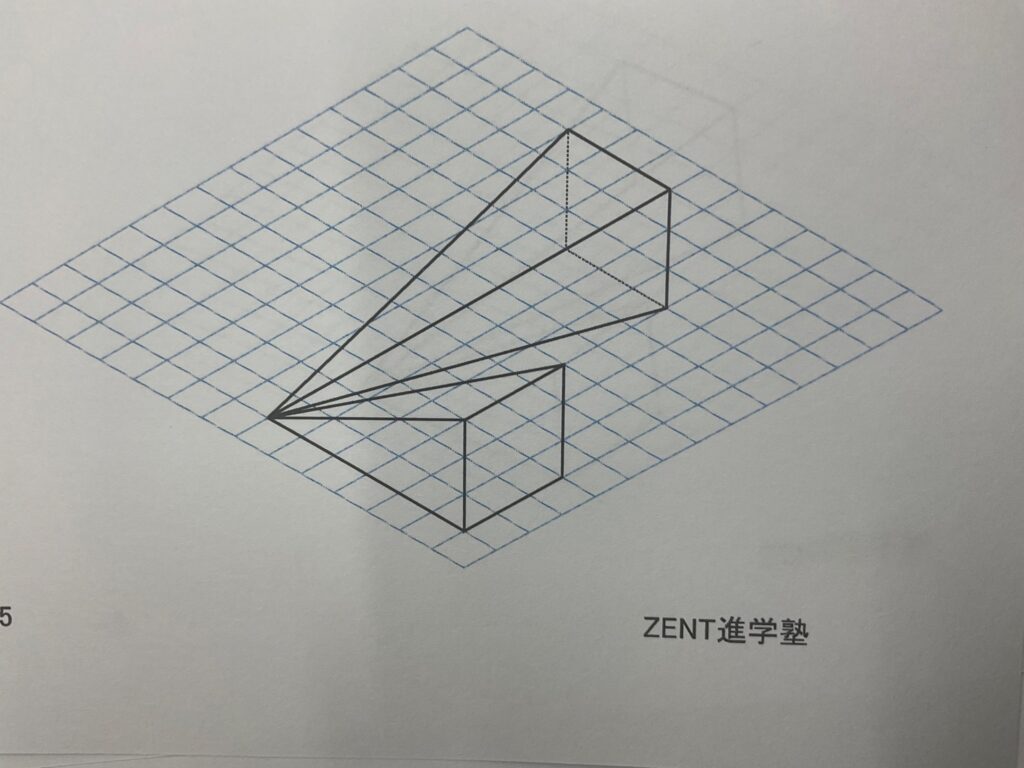
☝こちらの図形を「真上から見た形」を書いてもらいます。
この形はほとんどの小学生が苦手にしています。試しに挑戦してみてください。
前提条件は「一辺6の立方体の一部分を切り取った図形」です。
この辺までくると感覚だけで出来る子は難しいので、言葉を使って論理的に図を書く必要があります。
手順の前後に正解はありません。
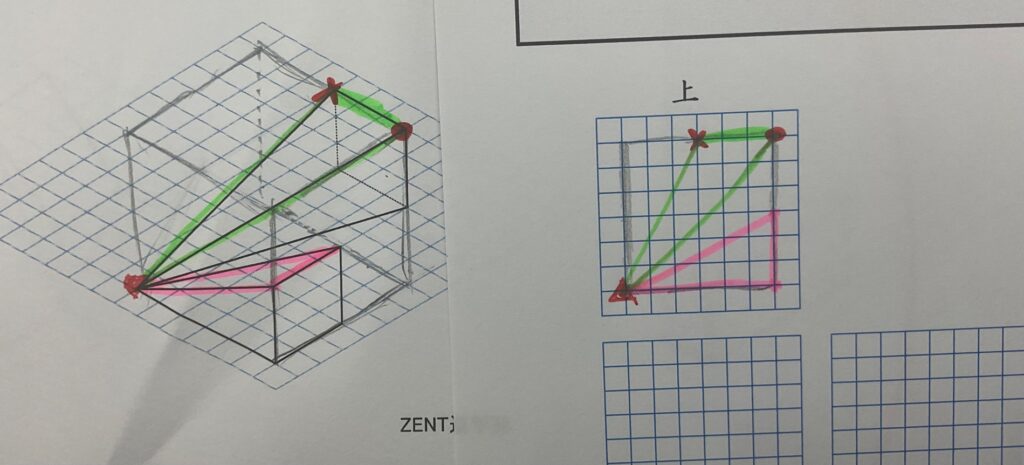
①一辺が6マスの立方体で図形を囲んでみる。
②●をかく。
③●から3マス左に×をかく。
④△の場所を決める。
⑤それぞれの点を線で結ぶ。
☝この一連の流れが、
・作図問題で「何を決めれば図が定まるか」が明確になる
・全体を一気に見ようとせず、局所（点）から考えられる
といった一例です。
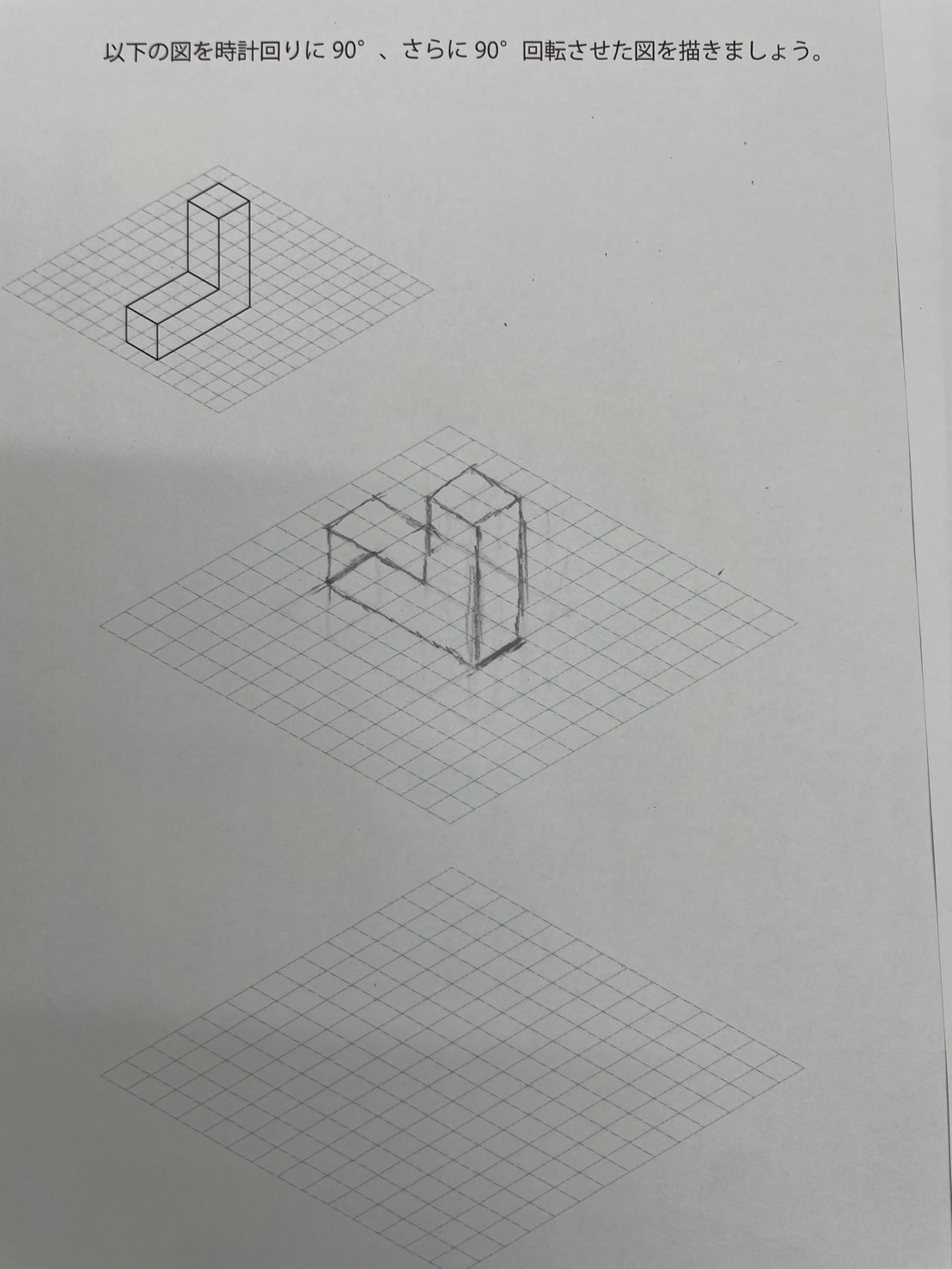
↓こちらの回転体の作図も同様のことが言えます。
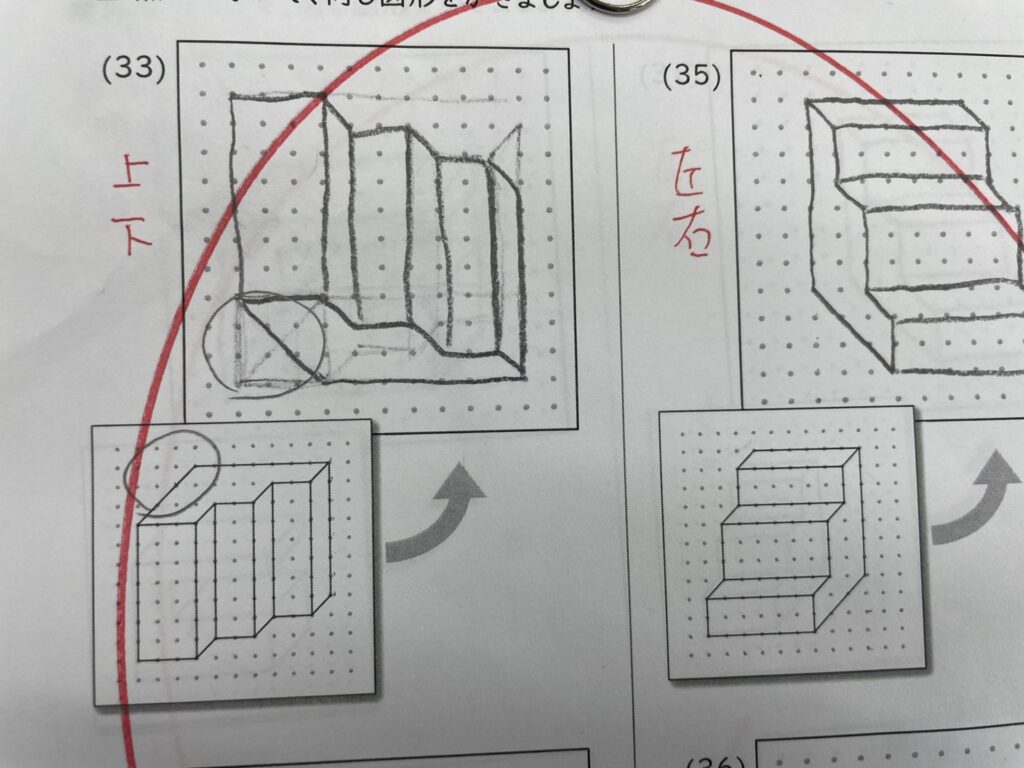
中学1次関数
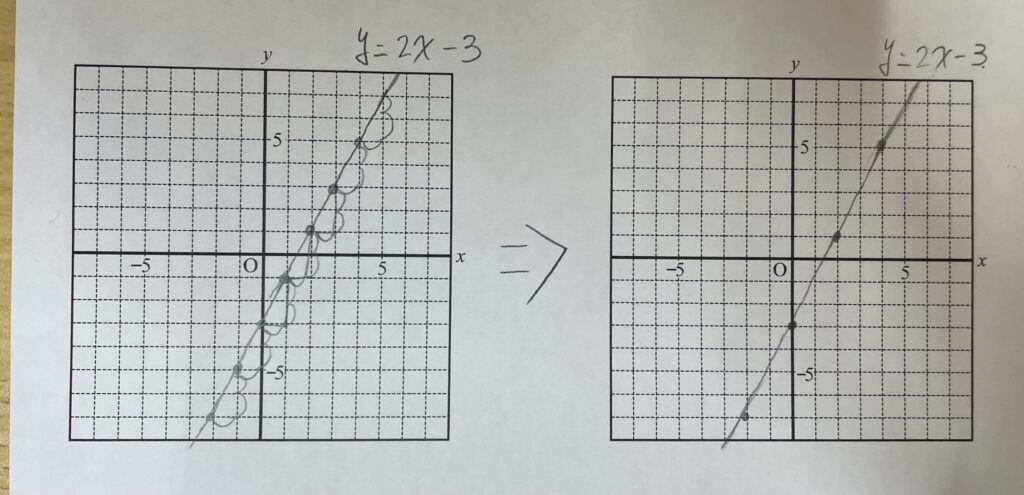
左のような書き方だと、関数を制することはやはり難しく、さらっと右ぐらいの雰囲気で書きたいですね。
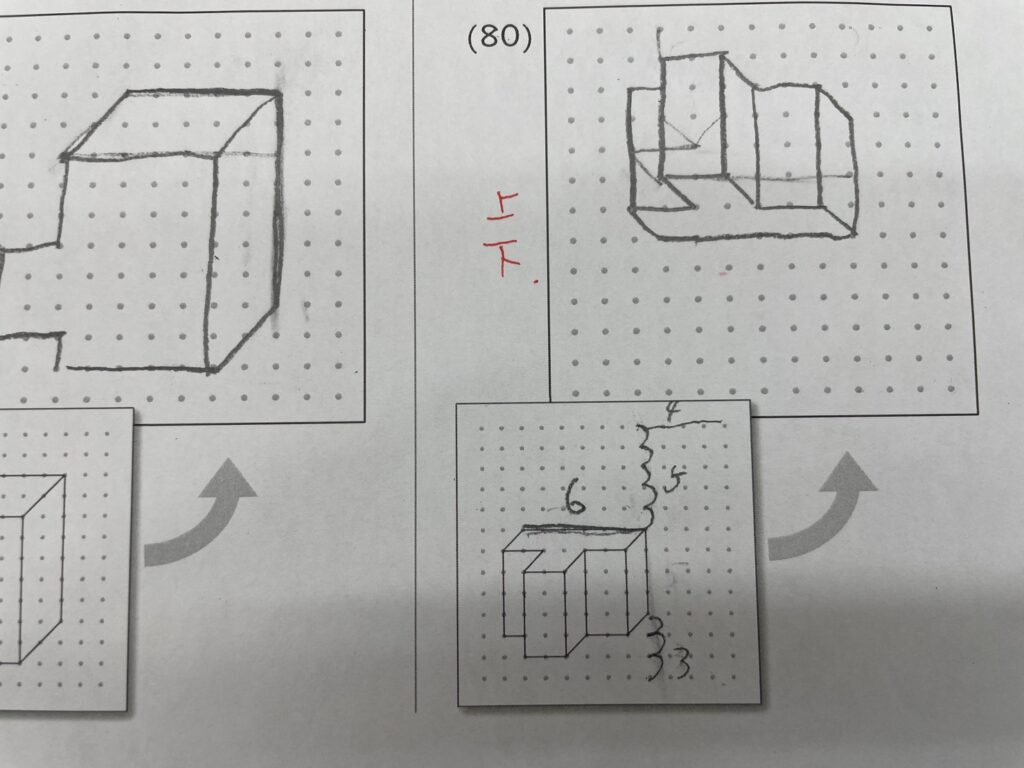
点描写レベルが、☝こういう感じだと、１次関数の習得にも苦労致します。
図形問題は、
・90度に見える
・なんとなくこれぐらい（論理の飛躍）
では出来るようにはなりません。
まとめ 図形はセンスではない
「図形はセンスのある子のもの」と思われがちですが、実はそうではありません。
図形問題で求められているのは、形そのものを見る力ではなく、位置関係や変化を数量として捉える力です。これは関数の考え方と深く結びついています。
点の動き、長さの変化、面積の増減を追うことで、図形は「感覚」から「構造」へと姿を変えます。適切な訓練を重ねれば、誰でも再現可能な思考として身につけることができるのです。
点描写に取り組まれている保護者の皆様、
よろしければ武田先生のプリントもルーティンと化して、
点描写のその先！
を体験してくださいませ。
この記事は、ゆるゆると更新してまいります。
たまに覗きに来てくださいませ。
公式lineからっ
ブログやお知らせなどをタイムラインにて定期配信中！気が向いた時だけブログを読めるようになっております( ´∀｀)
弊塾に対する相談・お問合せは公式LINEから！
