身体の発達と算数【非認知能力】指先の巧緻性

本日も張り切って参ります。


赤穂市の進学個別指導塾Willbeの光庵（こうあん）です。


幼児と算数というテーマから本日は、「身体の発達」「算数」「指先の巧緻性（器用さ）」という観点からお話しして参りたいと思います。




毎年、中3達は、数学/2次方程式/2次関数の点Pが動く問題に取り組んでもらいますが、Pに動かれるとパニパニです。高校生も頭を悩ます「点P」くんです。受験生の心の叫びは、常に「お願いだから点Pよ。動かないでおくれ」「aよ。常に定数のふりした変数ではなく、常に実数であってくれ（数Ⅰ：場合分け）」です。




大前提、私は天才を育てたい訳ではありません。


一見、勉強に関係ないことが、勉強の役に立つと言いたいだけです。


勉強や学力にはあらゆる要素が絡み合っているので、○○をすれば××になるという単純なことを言いたいわけではありません。私がお話しすることを見逃して、お子様の目に見える学力に固執することが不毛だということを申し上げたいのです。







さて話は変わって、

不器用さが算数に及ぼす影響

（教材は、エジソンクラブさんで購入できるプリントです。）

↑こちらは、小学3年生の点描写。



この子と出会って1年半。入塾テストは小学2年生にして20点。お母さんには「この子は計算が苦手だから算数が苦手だ」と教えていただきましたが、私には、はっきりズバッと行ってしまえばまだには勉強に向いてないということが分かってしまいます。それは点描写を見ればすぐに分かります。

小学2年生にして、この図を写しきれないのはまずいんだろうと思います。


だから、お母さんには「具体物に対する認知が弱いから待ってください」とお願いをします。もちろん、計算は計算で取り組むのですが、並行してこういったものに取り組んでもらう必要があります。


ちょっと成長が早い幼稚園児でも↑ぐらいの図形は正確に書けたりします。〇歳までに〇〇が出来るべきだと言いたくはないので、〇歳まで〇〇が出来ないなら訓練しながら待ってあげるべきだと私は言いたいのです。確かに、成長と共に身体性が追い付くこともありますが、何もせずに待ってあげても追い付くスピードは上がりません。


中学生でも同じような図を書く子はいます。そういう子は数字が少しでも変わると分からなくなったり、図形問題の解き方をまったく同じように暗記しなければならず、図形が変るとまったく分からなくなったりします。


しかし、私にはさすがに中学生になってから上記点描写をやってあげる勇気はありません。何よりも保護者様の理解が得られません。


決して遺伝などではなく、何年もかけて何年もかけて些細な習慣によって獲得してきた能力をたった1年～２年で追いつけるとは思えないのです。

おいつくために必要なことは紙の上の勉強（問題集/ドリル）だけではありません。

指先の巧緻性（器用さ）

一言で言うと、指先と手首が不器用ということです。


ポジショントーク過ぎて言いたくはないのですが、子ども達に指先や手首を動かす動作が日常から減ってきているので、不器用な子が増えてくるのだろうと思っています。


脳に繋がっている神経は、手首から指先にかけて繋がっているのです。

指先の動きをコントロールしているのは、主に脳の**大脳皮質（運動野）です。運動野の中でも、特に一次運動野は体の運動を直接的に指令する役割を持ちます。指先のような細かい動きを必要とする部分には、大脳皮質の中でも特に広い領域が割かれており（ホムンクルス図参照）、このことが指先の精密な制御を可能にしていま。。。

舌を噛むので辞めておきます

指先が器用かどうかは、触覚や位置感覚（固有受容感覚）も非常に大切です。触ったものの感触や位置を感じ取り、それに基づいて次の動作を調整します。たとえば、「どのくらいの力でつまむか」を微調整するのは、感覚情報が運動野にフィードバックされることで可能になります。

専門家ではないので辞めておきます。

まだまだ目の前にないものを頭の中に明確にイメージできるほど、イメージする力がないのです。こちらの小学生、1年前に比べると随分、点描写が上手になりました。おかげで文章題も苦手ではなくなりつつあります。


でも、


まだまだ待ってあげないといけないとあげません。







点描写だけで補える訳でもないのです。

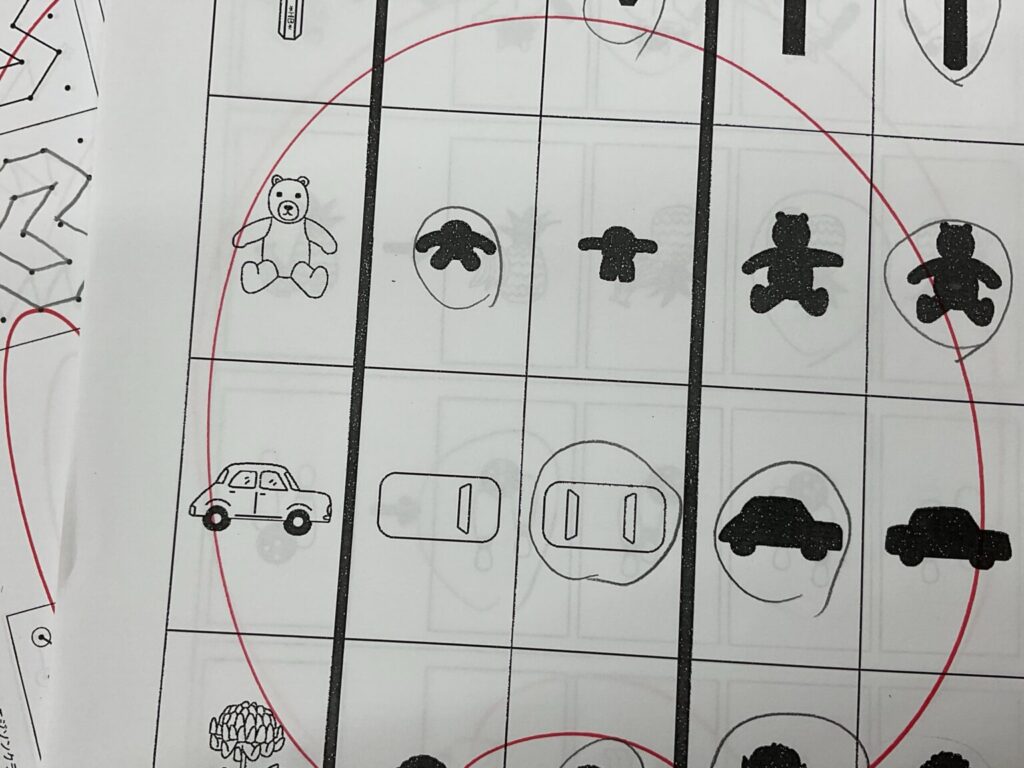
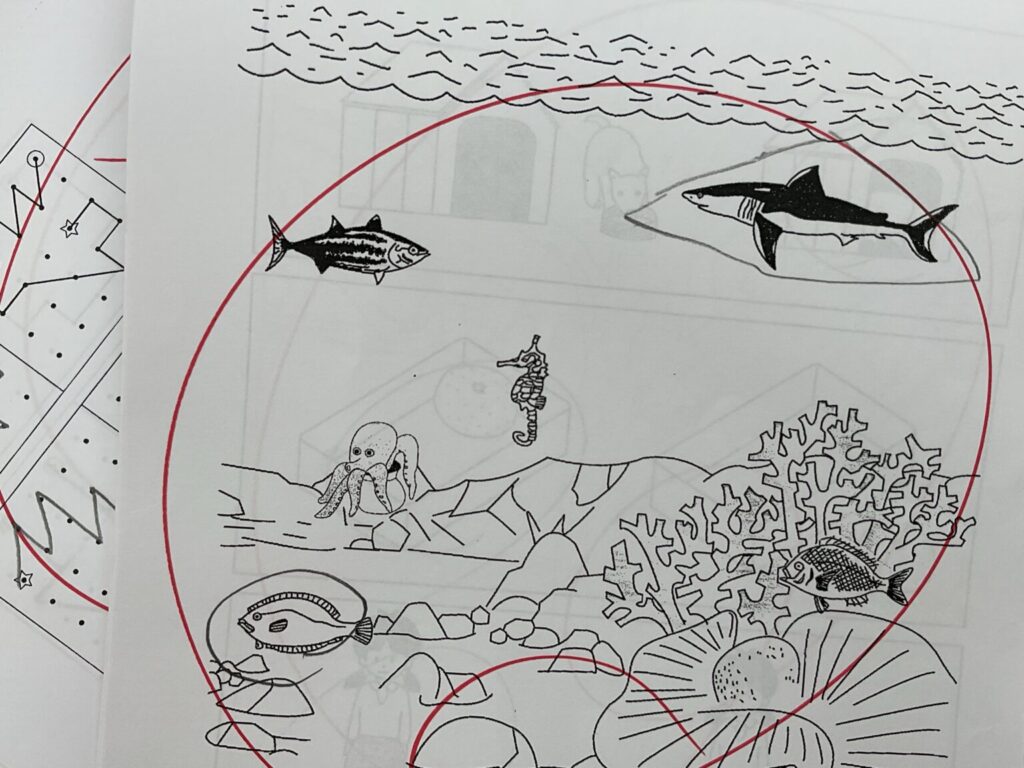
（こちらはピグマリオンさんの教材を使っています。）

もう少し、この話を続けると、


中学１年生「正負の計算」が苦手な子は、こういう左右対称といった感覚が苦手です。





正負の定義について、正確ではない説明をしますが、


0を中心に＋方向に順番に数えた数が＋5
0を中心にー方向に順番に数えた者がー５
どちらも「０からの距離」は「5」


です。

計算は出来ても、実際に長さの計算をしてみるとみんなパにパにです。簡単な問題は訓練できても応用ともなるとすべてを教えきれるものではないので、パターン暗記学習法を行うしかありません。


言葉と動作が一致していない場合は、習得するのに時間がかかるということを申し上げたいのです。


目の前の問題に正解するかどうかより、大切なことがあり、そういうものは幼児期～小学低学年の間に鍛えらえるということです。それが、たまに私が皆様にお伝えしている「後伸びする力」です。

まとめ

手首や指先が行き着く先

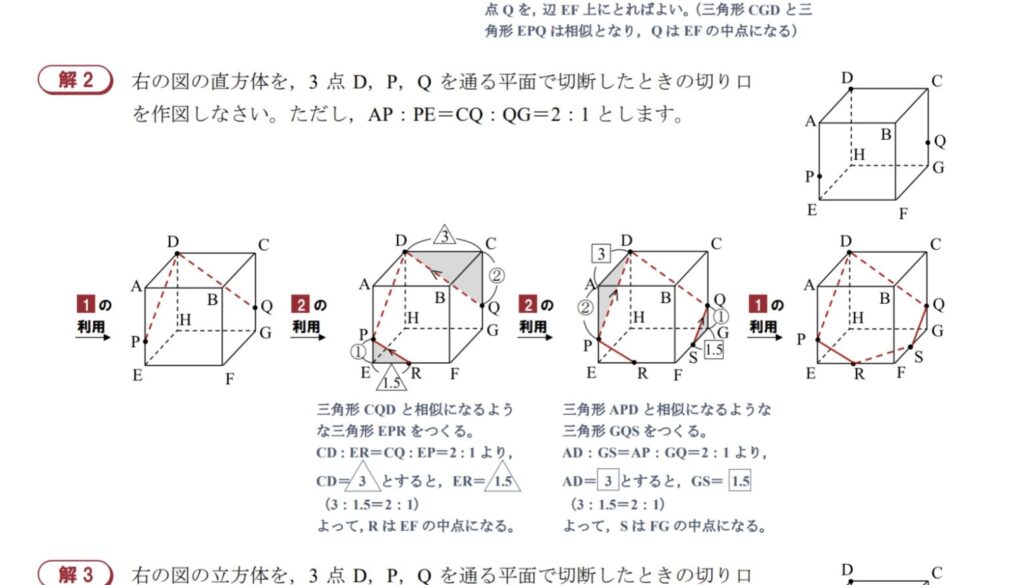
(https://x.com/nyushi_sugaku )「塾技」でおなじみの森先生のtweetからおかりました。

森先生が作成されている問題集の問題意識は、似たようなところがあると思っています。


上記プリントを図示できるかどうかで高校数学の理解度が決定的に変わるということが私の問題意識です。森先生は、上記図を丁寧にかけるプロセスを丁寧に説明されているように思います。


図形問題は、センスと言われがちですが、計算練習のような細かい訓練を細かくわけていく必要があるのですが、通常カリキュラムでは、図形も計算も丁寧に行うことが時間的に難しいというのが、集団授業の限界だったりします。


一方で、私が申し上げたいのは、図を書いたり「1：1の線分図」を正確に書いたりする前段階があるということでもあります。

普通を目指す子にこそ天才ドリル

追記します。