ここ１０年ほどで一気に学校に浸透した雰囲気を醸し出している
「さくらんぼ計算」。
保護者世代は、聞いたことも見たこともない計算方法。やりにくくて仕方ない。なんの意味があるの？出来たから何？
塾の先生もしらない計算方法。
今日は、親からすれば得体のしれない「さくらんぼ計算」について、小１～高校３年生まで教えている赤穂市の個別指導塾Willbe塾長の光庵が、さくらんぼ算についてまじめに考えていきたいと思います。
Willbeの小学低学年指導は、
①高校生が何の理解に苦しんでいるか？
②中学生がどんなことの理解に躓いているか？
③小学高学年がどこに悩んでいるか？
といった観点を集約したものです。
私は、サクランボ計算は、高校数学の「整数」という分野の根源だと思っています。
さくらんぼ算のやり方
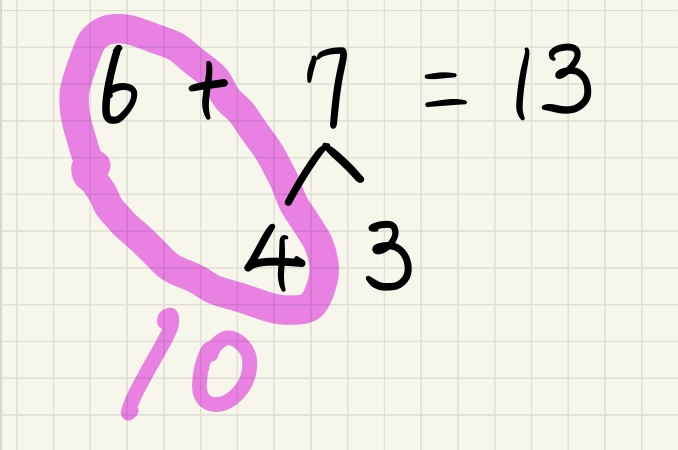
6＋7
6は10まであと4だから、
7を4と3に分解して、
4と6を10にする。
10と3を足す。
———————————
6＋7
＝6＋（4＋3）
＝10＋3
＝13
—————-
6＋7
＝（3＋3）＋7
＝3＋10
＝13
—————–
さくらんぼ算が出来ないとマズいのか？？
やらなければならないのか？？
そんなことはありません。
（繰り上がり繰り下がりの計算が）出来る子からすれば、「なぜこんな面倒なことをしないといけないのか不思議で仕方ない」と思うしかありません。お子様も保護者と同じ感覚ならば、問題ありません。
10×10＝100
↑これをひっ算で計算しなさいといわれて面倒くさいと思うのと同じ話です。
↑逆に面倒ですよ。
↑「やって」と言われてやれる必要はあるのかな？という程度です。
つまり、サクランボ計算をやってみてと言われて、教えて、出来ないならマズいのです
私も実は、筆算をやってといわれたら、考えながら出ないとできません笑
「いま何歳だっけ」と思い出す時の計算も、
「あれ？？18:10まであと何分だ？」って計算も、
2023-1989
＝23＋11
＝34
あ。34歳だ。
と計算します。
17:30-18:10
も筆算ではなく、
30＋10
＝40
あ。
４０分だ。
と計算します。
ですから、
小学生に筆算を教える時は、ちょっと筆算の手順を思い出してから教えます笑
だって、、、
使わないんだもん。
さくらんぼ算が出来ないとマズいのか？？
かなりマズいです。
繰り上がり、繰り下がりの計算で躓くことが目に見えています。
小学２年生～３年生が、「6＋7を指を使って数えているとマズい」というのはなんとなく大多数の保護者にご理解いただけるのではないでしょうか？
そして、指を使ってたし算をしている我が子をみて、
「あれ？？」
「この子は、”24＋13”をどうやって計算するんだろう。」と思うのではないでしょうか？
２４から順番に数えていくのでしょうか？？
指。。。
足りんよな。
と。
。。。。。。。
筆算で繰り上がりを冷静に考えると？？
↑
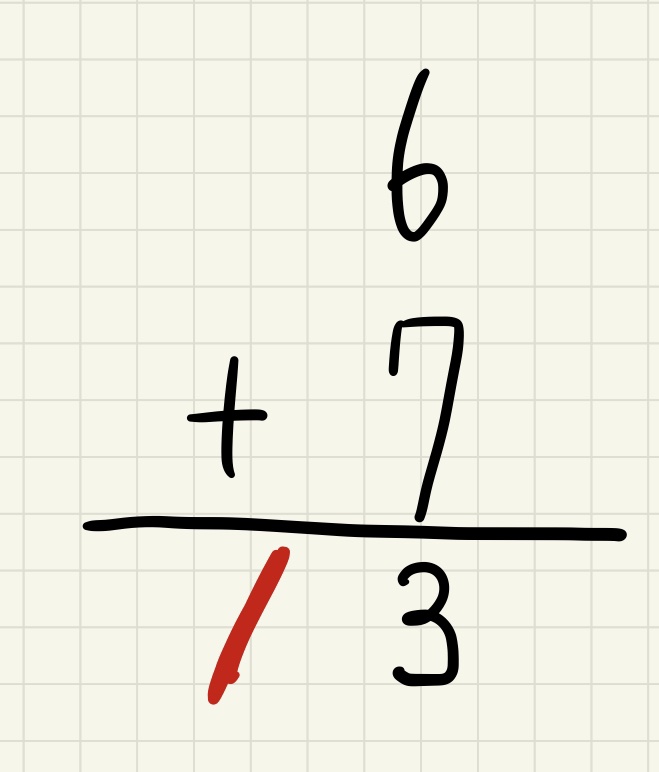
これって冷静に頭の中身を順番に紐解いていくとサクランボ計算していませんか？？
つまり、サクランボ計算が出来ないことが問題なのではなく、10をカタマリで捉えられてないことが問題なのです。
ひっ算も出来てる風を装って指で数えて、1だけ取っ払えば良いわけなので、ひっ算が出来ていそうに見えてもダメなわけです。
指、、、、
足りんよな。。。。
足の指でも使おうか。。。
うん？？
サクランボで躓くということは、筆算で苦労することが見えてしまうのです。
サクランボ計算が出来ない子は、何が身についていないのか？
①「量」と「順序数」の区別
順序数とは、、、、順番に数えていく数です。まさに指を使って数えていく感覚です。
「量」とは、区切りがよいマトマリ/カタマリで捉えれることです。
１L＝10ｄｌ
１m=100ｃｍ
1時間＝60分
1円＋１円＋１円＋１円＋１円＋１円＋１円＋１円＋１円＋１円
＝10円
これの何が難しいのか？？？
１円玉が10個で１０円やん？？
で？
１０円玉が１個で１０円やんか？？
うん？
いや。
で？
あら？
１０個と１個でなんで同じなん？？
子ども達ってそんな顔しません？？
ふてくされた表情で笑
ぷく～～～～～～～っ
ぷ～～～～
分からんっ
ぷいっ
んで
親は親で
親「はっ？ なんでこれが分からんのん？？」
親「いや、そういうもんなんや💢」
親「きぃ～～～っ」
②算数というより日本語？？
私と同じように小学低学年指導をされている先生（松江塾真島先生）の中には、
「数の概念」だとか「算数」ではなく「日本語だ」と言い切る方もいらっしゃいます。
この家の家族は？
兄弟は誰と誰？
食卓を目の前にして「今日のおかずは何と何？」
だとか
「〇というものは、△と×から成り立っている」
という日常的な会話を繰り返したうえで
「では、５は、2と×から成り立っている」
「×はいくつ？？」
と聞くとスルッと答えるはず。
↑↑
説得力があります。
私もそうだと思ったりします。
算数というのは、日常生活にありふれているので、日常でどれだけ具体的に算数っぽいことに触れるかどうかが重要な要素であるのは間違いないんです。
よく「悪の根源」みたく「昔と今は違うんだよ」と例示されるのが、お金ですね。
買い物なんて算数の勉強ですから、クレジットカードだと算数が身につかないよね！って話はよく聞きます。確かに説得力あります。
お金を使わなくたって算数は理解できるというのも本当ですし、やり方に関しては枚挙に暇がないわけです。
③いい感じに「分解」
さくらんぼ計算を苦しませている最大の原因（だと私が思っている）は、
「分解」です。
7＋6
6と3と3に分解する
分ける。
これなんです。
冷静に考えてみて、、、、「分ける」という行為を小学校１年生の算数でやるだろうか？？
小学校１年生の教科書には載っています。
7は3と〇です。
みたいな場所です。
でも
計算ドリルを見てみると、
「合わせる」「減る」が大半だと思われます。
分解。。。。
さらに、、
日常生活において、、、
分けるという行為。
「分解する」という行為
あまり思いつきませんね笑
でも、あるでしょうね笑。
どちらかというと、、、
「分解」「わける」ということをやって欲しい問題集で、かぞえて乗り切っている場合が、厳しいのかなと思ったりしています。
サクランボ計算に躓いている子に何が必要なのか？
①鬼のプリント反復練習
それこそ公文のように。
プリントを使って筋肉で理解する笑
これでもかと笑
これはこれで好きです。
どんな方法を使ってたとしても、
数式なんてもんは、あらゆる無駄をそぎ落として究極的にスリムに抽象度高く表現しているものですから、
2＋3を具体で語ろうと思えば、、、、
１億を超える具体例がでてくるでしょう。
だから、
理解はあとで良い！
まずは出来ること優先！
やり方を伝え、
マネして、
反復する、
これはこれで大事なこと。
②〇〇づつ数えるの訓練
さくらんぼ計算が疎い子は、
間違いなく「量」に関する訓練が足りてないわけですから、
「量」の訓練をするのです。「順番」と「量」は違うのです。これは思っているより難しいのです。
ビー玉を５個ずつ数える。
ボードゲームのような何かしらのポイント計算をする。
野菜を半分にきる。
（１個をきっても１個が２個出来る）
桜の花びらを２個づつ数える。
に～し～ろ～は～とぉ～～～～
ご～じゅう～じゅぅぅぅぅごぉ～～～にぃじゅ～～
などなど
↑これ重要です。
小学校の教科書をみてみると
「〇個づつ数える」の後に「サクランボ計算」が登場しています。
だから、
サクランボ計算って２年生なんです。
Willbeはどちら派？？
①反復練習
②〇個ずつ数える
両方ですね。
①のプリントはあまり使いません。
プリントってやはり高度なんですよ。
「さくらんぼ計算が出来ない子何が足りないか？」と考えたときに、「日本語と量」のどちらも説得力があるわけです。
そして、
いずれも
「反復」していることが重要なんですよね。
「反復」というと「ドリル」のようなものをイメージしてしまいますが、
あらゆるモノを使って、
あらゆることで反復する
のが正解なんです。
具体物を使いまくって、
小学１年生の教科書に載っている言葉を使いまくって、
反復して、
言葉が定着したら、
プリントでも良いのだと思います。
そもそも、、、
具体物を使った方が、会話がふえる！！！
まま。
Willbeは個別指導ですから、
人によってやってることは違います。
結論
小学校も進級式ですから、
いつのまにか「サクランボ計算」なんて言葉は忘れていきます。
でも、、、
サクランボ計算は出来た方が良いに決まっています。
なぜなら、
ひっ算でも躓くだろうし、
時計も躓くだろうし、
〇個あたりって言葉にも躓くだろう。
極論でやや誤解があるのですが、
小学校高学年で
ひっ算を多用する子は、
伸びない傾向にあります。
個人差ありますよ笑？
ポジショントークだと思ってください。
何故なら？？
23×6
のような単純な計算を瞬殺で出来るような訓練もしていなければ、
（20＋3）× 6
＝120＋18
＝132
といった工夫も出来ないのですから、
新しいことを定着させるのに、
人より時間がかかるわけです。
中学校の数学、
23×6をひっ算使ってたらそりゃしんどいよね。
１時間あたりにこなせる問題量も減るよね。
正負の計算も理解せずに暗記するしかないんだと思います。
正負の計算って、
冒頭で申し上げた、↓こういう考え方を多用します。
2023-1989
＝23＋11
＝34
あ。34歳だ。
と計算します。
———————–
18：10-17：30
もひっ算ではなく、
30＋10
＝40
あ。
４０分だ。
と計算します。
小学校４年生までの算数をどれほどの高い精度で出来るかどうか。
それが小学５年生～中学３年間の算数/数学を左右します。
小4～小６にさくらんぼ計算をどう生かして欲しいか
さくらんぼ計算は、小学２年生？でしか取りざたされませんが、実は高学年になって威力を発揮します。
250＋72
＝250＋（50＋22）
＝300＋22
＝322
321＋81
＝(300＋21)＋(79＋2)
＝300＋100＋2
＝402
こういった感じでしょうか？？
筆算いりません。
これはテクニック/やり方といった言葉ではなく、
10のまとまりの理解、さくらんぼ計算の重要性
といった方がよいのではないかと思います。
合わせてよみたいピアノ講師の算数日記
ブログやお知らせなどをタイムラインにて定期配信中！
気が向いた時だけブログを読めるようになっております( ´∀｀)
弊塾に対する相談・お問合せは公式LINEから！
ただ、、、
これが
ポジショントークだと私が申し上げているのは、
今日お話しした内容のすべては、
ほぼ日常生活で使っているのです。
ですから、
塾に行かなければならない必然性はないのです。
小学１～3年生 生徒募集中
毎週水曜日
16：30～18：20
（途中10分休憩）
具体物を使って数を理解する。
ブログやお知らせなどをタイムラインにて定期配信中！
気が向いた時だけブログを読めるようになっております( ´∀｀)
弊塾に対する相談・お問合せは公式LINEから！