基礎が大事というのは簡単だけれど【数学】

基礎が大事である。


私はそれしか言いません。


このブログ、


「基礎が大事というのは簡単だけれど【数学】」


を、


一生懸命問題演習するのだけれど、
高校入試偏差値数学60に到達するかしないか、
それぐらいの子


に読んで欲しいと思って書きます。

陰謀論と歴史認識、そして数学の話

誰でも陰謀論に巻き込まれる可能性はあります。

陰謀論と歴史認識は、とてもデリケートな話題です。
正直、扱いにくい。

ですが、

• 陰謀論を信じてしまう
• 事実ではない歴史（＝物語）を信じてしまう

こうしたことは、誰にでも起こりうると私は思っています。

人間は、
「スッキリしたい生き物」
だからです。





人は、

・自分の興味が自分にとって難しすぎる時、
・ただただ楽しみたいとき、
・人気者になりたいとき、
・誰かをコントロールしようとするとき、

物語を作り上げます。




私自身もリテラシーが大事と言いながら、

私の信じているものが「陰謀論」である可能性にビビりながら

生活しています。

私たちが「好き」だと言っている歴史の正体

大前提として。

歴史好きと称される人たちが好んでいる歴史は、

ほとんどの場合、

「物語＝小説」

です。

間違いなく、
私自身もそうです。

歴史の大半は「物語」である

歴史の大半が「物語」であると認識できていれば、
特に問題はありません。

大人であれば、

• 事実ではないと分かったうえで
• 「物語」として楽しむ

それでいいのです。

子どもが大河ドラマを見て、
「これが本当の歴史なんだ！」
と思ってしまうのも、私は許してあげていいと思っています。

三国志も大河ドラマも「事実」ではない

三国志にしろ、
大河ドラマにしろ、

事実ではありません。

多くの部分は、
創作です。

そこにあるのは、

• そうであってほしい
• そうだったら面白い

という願望です。

英雄が「英雄」であってほしい理由

例えば、豊臣秀吉。

偉業を成し遂げた「英雄」だからこそ、
「そうであってほしい」という願いが生まれる。

また、
そうでないと困る人もいるでしょう（笑）

これは数学でも、まったく同じことが起こる

実は、
数学でも同じことが頻繁に起こります。

特に、
図形問題で。

「そうあってほしい」から過程が作られる

願望が先に立ち、

「きっとこうだろう」
「たぶんこうに違いない」

という思い込みから、
過程が後付けで作られる。

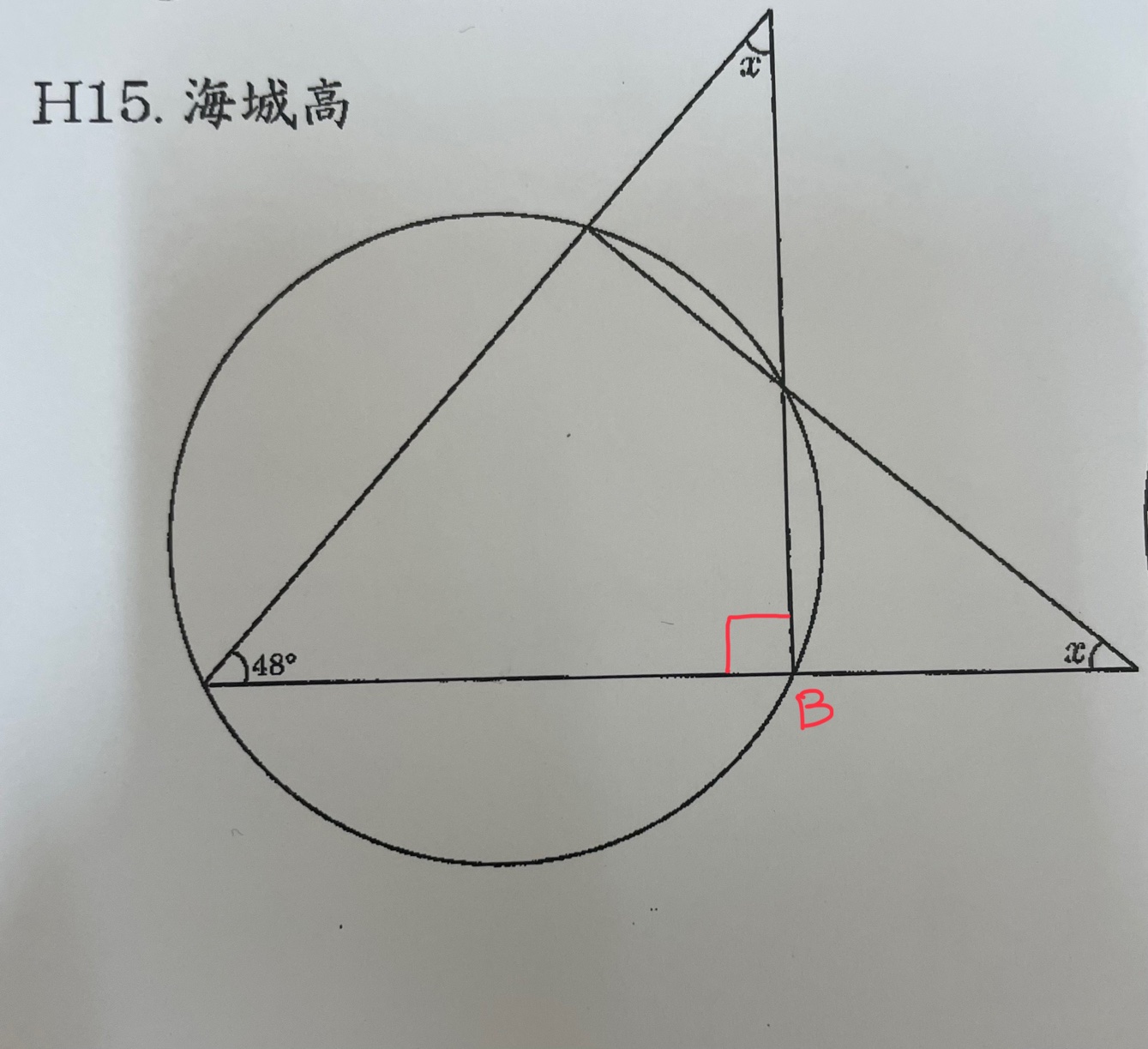
例：∠Bは90度である

この「xの角度を問題」で与えられている条件は、黒い部分のみです。





∠Bが90度である。

これは、
事実です。

しかし問題は、
その過程です。

見た目で判断した人

見た目で判断した人は「そうあってほしい」という願望によって「90度」だと言っています。


問題で与えられている条件を見ても、そんなことは分かりません

もしかしたら89度かもしれません。

結果が合っていても、それはアウト

「こう見えちゃった」

これ、ダメです。

結果的に合っていても、

• 直径（円の中心をとおる直線）だと判断できる理由がない

故に、
正解ではありません。

あなたの「願望」

もし、

∠B＝90°

だと分かってしまえば、

180 − (48＋90)
＝ 42

と、
一瞬で解きたくなりますよね。

ちなみに、
x＝42°
答えは正解です。

定理が使えるっぽくね？？という願望

図に書いてある情報を無視して、

• 赤い△を勝手にイメージし
• ∠B＝90°だと言ってしまう

この「なぜダメなのか」が分からない人は、

円周角の定理

を、
本気で復習してください。

「○○っぽい」は数学では通用しない

数学は、

「○○っぽい！！」

ではダメです。

高校入試数学偏差値60に届かない理由

おそらく、

偏差値60に到達しない人の多くは

正解しているが、過程が間違っている

ケースが非常に多い。

申し訳ありません。
うちの塾でも、

数学偏差値65に届かない子たちは、

間違った過程なのに○をつけている

ことが本当に多いです。

お説教です（笑）

なぜ、
こういうことが起こるのか。

答えはシンプルです。

当たり前への「解像度」が低い

当たり前のことに対する解像度が低い。

2×3＝6 は、なぜ6なのか？

2×3＝6

これは誰でも知っています。

でも、

なぜ、2×3は6なのか？

この問いに、
ちゃんと向き合ってほしいのです。

（まだ数学に慣れていない小学生ならば100歩譲ります）

賢い子の共通点

賢い子は、

• 基本的な定理

に対する
解像度が異常に高い。

当たり前（基礎）を、ねちっこく

当たり前のことを、

• ネチッこく
• ねちっこく
• しつこく

「なんでなん？」と問いかけ続ける。

正直、
しんどいよね。

嫌なのも、
よく分かっています。

でも、今やっている勉強は…

でもね。

君たちは今、

• つじつまを合わせる勉強
• 結果から「そうあってほしい願望」を想像するクセ

を、
知らず知らずのうちに身につけている。

だから言います

だから、

点数が高い＝頭が良い

とは、
ならないのです。

簡単な問題＝基礎ではない。

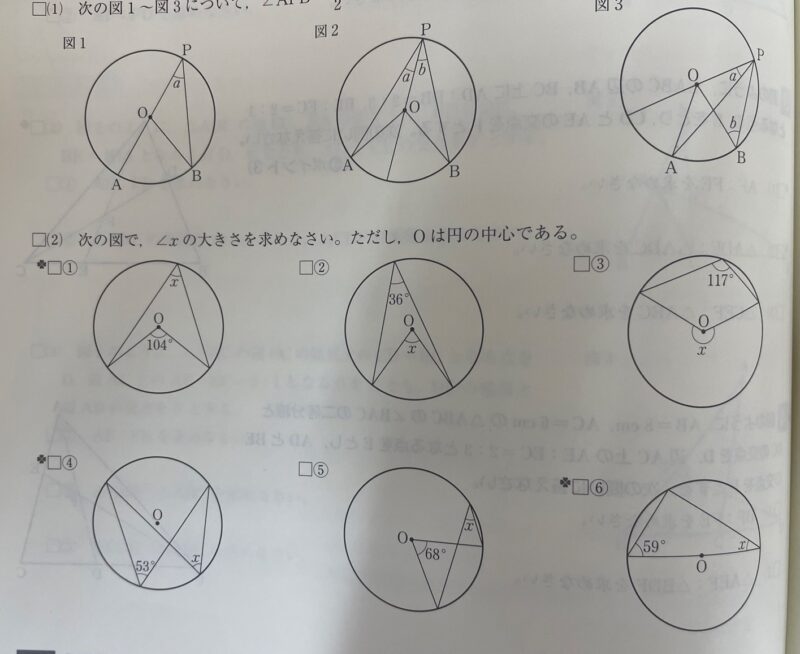
上記（1）（2）は基本問題です。

(1)次の図１～図３について、∠APB＝1/2∠AOBが成り立つことを、文字を使って示しなさい。

どちらかといえば、（1）の方が重要だと私は思っています。

簡単かどうかは分かりません。

(2)のように簡単な問題には、
厳密なプロセスはほとんど登場しません。

（0.1秒で解く瞬発力は必要だけどね…😢）
（だから難しいんだけど）

（2）を（1）っぽく説明出来たりする力が、

もう少し複雑な問題において「補助線」が見えるような力

を身につける気がしています。

高校受験数学の真実

簡単な問題（正答率60％程度の問題）を
一つも落とさず解き切る。

それで、
偏差値60に到達する。

それが、
高校受験数学の現実です。

しかし、
それでは先が見えるのです。

故に、
私は中学基礎を
兵庫県公立高校入試偏差値65程度だと言っております。

リテラシー/論理的思考力とは？

記事の途中で☝このように申し上げました。


そりゃ人生のうちで「おみくじに身をゆだねるような決断力」が
必要であることは疑いの余地がありません。


試験本番でのラッキーパンチを否定もしません。


社会や国語で学ぶ「リテラシー」「論理的思考力」とは、
いままで記事に書いてきたようなことなのです。


「目の前の正解」「目の前の点数」にとらわれ過ぎると、
見えない力を失うと言いたいのです。


見えないのだから気が付かないのです。